"There must be a proper theory of place other than 'To Find Kalamazoo, look in F3'."--from Euclid's Window, The Story of Geometry from Parallel Lines to Hyperspace, by Leonard Mlodinow
 |
| You Are Here...There...Everywhere |
To determine Latitude,
imagine a Little Earth, and 3 Little Points.
{This should sound familiar to You, since You dreamt it when You were 8}.
Take one point P1 and put it at the North Pole, and the second point P2 and put it at the Center of the Little Earth, and use the third point P3 to Mark where you are on the Little Earth.
Now draw a line from the North Pole straight through the point at the Center, to the other end of the Little Earth. This First line, Line 1, forms the Little Earth's axis of Rotation.
Then draw a line from the Point where You are standing through the point at the Center of the Little Earth, Line 2, to form an angle,
α , with the Little Earth's axis of rotation, that first line You drew.
The two lines act like a Protractor and that angle
α is a generic way to determine Your Latitude.
 |
Determine Latitude Using
The Little Earth
A Portion of the Fano Plane |
Which is a great way of thinking of where You are, but will not help Us
find each other.
For that We have to imagine a Big Earth (Way Way Bigger than Our Little Earth).
Something on the Cosmic scale, that would be the Celestial Sphere, the map of Stars that circles the globe.
Imagine the Big Earth around the Little Earth, the globe that is now the Core (where You are standing & spinning) of the Celestial Sphere.
This will help to determine Longitude, sinceYou are not a
Flatlander and need at least these 2 coordinates to determine where You are exactly in 3D.
Remember, since the Earth Rotates
360 degrees in 24 hours, the Stars over Your head are going to move about 15 degrees every hour, so that someOne standing West of You will See the Same Sky an hour later. Which has direct associations to
the Fano Plane (diagram below. see also
'kissing circles' and
Appolonian Network):
If You are at the Equator (to help me do the math) that translates to distance of about 1000 miles in that much time.
So, You look up at the Sky over where You are standing, and pick a star--any star, that You may be familiar with and note the local time it rises above the horizon, its Right Ascension (RA).
The reference, or baseline is the star γ Aries at 0 hours RA, the First Star in Aries where it crosses the Celestial Equator on the First Day of Spring.
Since there are Apps for this, just point Your PDA at Triangulum Australis, I think He Said 'The Second Star on the Left' and make a note of its RA in Hours-Minutes-Seconds (this presumes that You may be somewhere in the Southern
Hemisphere of the Little Earth).
{But if I got that wrong, since I heard this while under duress, and wish I had written it down to be sure so many years ago, make a note of the Second Star on the Right RA , too.}
No matter what, He Will Find You. You already know His Voice, so don't think too much about what He may look like, since there is usually some type of distortion due to Projection, but I can assure You, He is either Your Heavenly Father or Your Brother, and Either One will take You where You belong--to be with the Ones who love You.{Knowing that no matter who or what it is You think is going on around You, and what ever disinformation or misinformation is propagated through rumor mills or media channels, they are collectively Nothing but Remnants, Effigies, Residue of things and people gone by, because they lie in order to sever Our Ties of Kinship and in so doing work corruption on the Little Earth
فَهَلْ عَسَيْتُمْ إِن تَوَلَّيْتُمْ أَن تُفْسِدُوا فِي الْأَرْضِ وَتُقَطِّعُوا أَرْحَامَكُمْ (47:22
47:22 Would you, perchance if You were given Dominion in the Earth, work corruption and Sever Your Maternal Bonds (bonds of kinship, literally, 'sever/cut off Your wombs/matrices/'Places of Mercy')?
Which is exactly what they do when they spread their conspiracy theories of UFOs and aliens.
Recall that God made everything first, then He Created the Human Being--meaning that the Human Being was to be the Ultimate Creation--meant to Evolve or Reach the Highest form of Creation, but now what have We?}
And the reason that no matter how far You wander off or how big the Universe gets, it's no big deal for Him to find You?--The simplest, 2D planar point group, the Fano Plane PG(3,2)!
{I just answered my own question, must be another from of insanity}.
Can You imagine how it feels to an ant when it ventures off that ant hill? Apparently, even the ants know that As Above, So Is Below...{oops, did it again.}
And He Probably Triangulates with nothing more sophisticated than using 2 Dimensional finite geometry to wend His Way throughout the 'flat, not moving Earth' and the infinite (Multi-Dimensional) Cosmos--->
What is the simplest, smallest, ...perfect universe...a complex universe of breathtaking, abstract, beauty...consisting of only 7 points, 7 lines and their dual?
{I'll let someone who knows what He's talking about answer that one..}
According to one Mathematician, (paraphrasing):
'The 2D planar point group, the Fano Plane PG(3,2) is......the smallest, perfect universe...a complex universe of breathtaking, abstract, beauty...consisting of only 7 points and 7 lines; the smallest project space over the field Z2 with 15 points, 35 lines and 15 planes.
A space whose overall design incorporates and improves many of the standard features of the 3D Euclidean space we think we live in..the smallest 3D projective space...that plays an important and core role in many fields of mathematics, inlcuding combinatorics, group theory, and geometry'--Burkard Polster, 2001
In non-Euclidian geometry parallel lines meet (
intersect) at a point (just like when drawing a perspective of train tracks on paper, they seem to meet at the 'vanishing point'), and
that is why the Fano plane is a good 2D small-scale model of the larger 3D Celestial Sphere with the Little Earth at its Core (Your 'Big Earth/Little Earth' dream).
In fact, the Fano plane is the smallest
projective plane and probably why the Pyramids were built and are still standing. And it is no mere chance that the projective plane is sometimes called a
'twisted sphere'--'a surface without boundary derived from a usual plane by addition of a line at infinity.
'Just as a straight line in projective geometry contains a single point at infinity at which the endpoints meet, a plane in projective geometry contains a single line at infinity at which the edges of the plane meet.
A projective plane can be constructed by gluing both pairs of opposite edges of a rectangle together giving both pairs a half-twist (The Reverse would be Unfolding such a surface). It is a one-sided surface, but cannot be realized in three-dimensional space without crossing itself.'
 |
| Projective Plane From A Sphere |
A finite projective plane of order 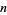 is formally defined as a set of
is formally defined as a set of 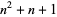 points with the properties that:
points with the properties that:
1. Any two points determine a line,
2. Any two lines determine a point,
3. Every point has 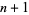 lines on it, and
lines on it, and
4. Every line contains 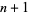 points.
points.
(Note that some of these properties are redundant.)
A projective plane is therefore a symmetric (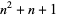 ,
, 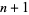 , 1) block design.
, 1) block design.
An affine plane of order 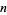 exists iff a projective plane of order
exists iff a projective plane of order 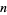 exists.
exists.
 |
Bizarro Comic August 21, 2012
Innie_ Audi Belly Buttons |
The
3 points at each vertex of the triangle defining the Fano plane, represent these vanishing points (You took technical drawing classes so You get this). They serve to define
'Outside' because, as You know, there is no way to define the 'Inside' without
SomeThing or SomeOne being on the 'Outside'.
{kind of like there is no way to know Up from Down in outer space; now, You know why You were so facinated by your belly button when You were 2 years old}.
But since we are still biding our Time in the 'Real' world,
having missed our ride out of here so many years ago,
I suspect we are to put this to more pragmatic, concrete use than just appreciating its abstract beauty---I mean, really,
what do mathematicians know? --they, too, are still stuck on the ground.
The Lehmers (1974) found an application of the Fano plane for factoring integers via quadratic forms. Here, the triples of forms used form the lines of the projective geometry on seven points, whose planes are Fano configurations corresponding to pairs of residue classes mod 24 (Lehmer and Lehmer 1974, Guy 1975, Shanks 1985). The group of automorphisms (incidence-preserving bijections) of the Fano plane is the simple group of group order 168 (full automorphisms== 7 generators x the 24 automorphisms of the tetrahedron symmetry group).--excerpt from Wolframalpha
 |
Argyle Sweater August 24, 2012
Rand & McNally Cartogrophers Extraordinaire |
A long time ago, Ptolomy published
Geographia, and used a similar method, like stereographic projection, to represent
the Earth as a Flat Surface, and he used
Latitude and Longitude coordinates to locate about 8000 places he knew of at the time and gave instructions for map making (cartography).
It served as as standard reference for 100 years, but made no progress under Roman rule. When a Christian mob sacked the library at Alexandria,
Geographia disappeared along with other math and Greek works (never mind how they disposed of the Greek worker Hypatia).
With the fall of the Roman Empire, "the new age found a civilization as much in the dark about describing their place in space as was about the theorems and relations among spatial objects."--
That's why We take care of books...
Anyhow, using
'irrational' numbers was also lost and this
'bad math' did not resurface until Cantor and Dedekind rediscovered it in the late 19th century (that's probably the punishment they deserved for what they did to Hypatia).
From the Middle Ages until that time scientists and mathematicians had been using them "happily, if awkwardly, anyway for the simple reward of getting the right answer outweighing having to wield unpleasant numbers 'that did not exist'."
This 'illegal' math is quite common today and we take it for granted.
There was also Dirac's delta function which posed a quandary for mathematicians; one that is simply =0 everywhere except at 1 point, where the value is infinity, but when applied in calculus or certain math operations typically gives us finite non-zero answers. Then the mathematician Laurent Schwartz (one more thing we can thank the French for) came along and showed that 'the rules of math can be redefined to allow using the delta function, opening up a whole new discipline of math and later buttressing 'illegal' physics concepts like quantum field theories, as well.
As of 2001, no one had yet successfully shown that, 'mathematically speaking, such theories legally exist.'
An antipode to the stance taken by the general population, and teenagers (who think they know everything) without stopping to consider that even the greatest minds throughout history had reason to know better.
When we next see each other, You can let me know if You had chanced on anyone of that ilk.
The story continues, that
Decartes translated space into numbers (quantitatively, not simply by construction), or
phrased geometry in terms of algebra. Decartes distance formula being deeply tied to Euclidean Geometry and
key to understanding both Euclidean and non-Euclidean geometries; serving as the basis for much of his contribution to physics.
Yet, Rene delayed publishing for 19 years--in fact, "...he delayed publishing anything until he was 40. What was he afraid of? The usual suspect. The Catholic Church."
"Through the centuries, mathematicians who attempted to prove the parallel postulate (Euclid's 'parallel lines never meet') as a theorem came close to discovering a strange and exciting new kind of space, but each of them was hampered by a simple belief: that the postulate was a true and necessary property of space."
...everyone but Gauss, who basically acceded to his own observation that a line is a curve of some sort, rather than clinging to Euclid's postulate, which in turn led to the rediscovery of curved spaces. A property that Gauss had to propose when applying the basic tenet that "superposition is a way to check for congruence or equivalence of geometric shapes."
There are other examples of
non-Euclidean geometries.
In turn, Poincare developed his model of
hyperbolic space, which was not just the 'model', but
hyperbolic space in 2D, concluding that
all possible mathematical descriptions of hyperbolic planes are isomorphic, in other words, 'the same.'
Poincare's lines are analogous to great circles, a rediscovery of what
the Ancients knew about geodesics. The Equator being a curve of constant latitude.
"The view from outer space is not the view of the indigenous people of Noneuclid (a fictional professor sending her students out to measure distance across the globe). To her, there is no 'center of the earth', and as Gauss showed possible, there is no 'outer space.'...the space...is non-Euclidean, not hyperbolic space, but the space appropriate to the surface of the globe: elliptical space."
Meaning, the great circles intersect, and the sum of the angles of the triangle on such a surface is greater than 180 degrees, (as compared to that for hyperbolic space being less than 180 degrees, and for Euclid in a plane it is equal to 180). The Geo-
metrics that define what we think of as 'hyperspace',
'subspace', and
'flat earth'.
And these concepts laid the foundation for Riemann's differential geometry in 1915, in the vernacular having to define 'place vs. space', where place is 'part of a space' occupied by a specific object:
"The question of the valididty of geometry...is related to the question of the internal basis of metric [distance] relationships of the space...we must seek the ground of its metric relations outside it, in the binding forces which act on it..."--Georg Friedrich Bernhardt Riemann
And then breakthroughs by Klein, Piola, and Hilbert following soon after, applying
tensor mathematics and algebraic curves.
Godel's theorem proved that
in a system of sufficient complexity, such as the theory of numbers,
there must exist a statement that cannot be proved either true of false.
A corollary of which:
There must exist a true statement that cannot be proved.
Example: There Is A God.
And all this ground-breaking, thought-provoking, formulations, rediscoveries and challenges swung like a pendulum back to the
Flat Earth, again, considering what Clifford had proposed in 1870:
William Kingdon Clifford maintained:
"I hold in fact:
- That small portions of space are of a nature analogous to little hills on a surface which is on average flat.
- That the property of being curved or distorted is continually passed on from one portion of space to another after the manner of a wave.
- That this variation of the curvature of space is really what happens in that phenomenon which we call the motion of matter..."
And while Clifford professed his position based on instinct alone, he got it right! Which in turn inspired Einstien's space-time and warpage ideology encapsulated in his Relativity theories.
Eventually leading to concepts like supersymmetry and string theory.
As for them-thar-hills Clifford was intuitively talking about-- be they mounds, mountains or dunes...Quran anticipated someone wondering about them.
Surah 20 TaHa (طه )
طه 20:1
20:105 وَيَسْأَلُونَكَ عَنِالْجِبَا
فَقُلْ يَنسِفُهَا رَبِّي نَسْفًا فَيَذَرُهَا قَاعًا صَفْصَفًا 20:106
20:107 لَا تَرَى فِيهَا عِوَجًا وَلَا أَمْتًا
20:108يَوْمَئِذٍ يَتَّبِعُونَ الدَّاعِيَ لَا عِوَجَ لَهُ وَخَشَعَت الْأَصْوَاتُ لِلرَّحْمَنِ فَلَا تَسْمَعُ إِلَّا هَمْسًا
20:1 Tta.Ha
20:105 They'll ask You about the Mountains/Hills/Highlands/Barrows
20:106 Say, "God Will Level them Flat (Blast/Torpedo them Flat/To Sinking); Leaving it a level plane (Leaving it bottoming (simply) wasting)
20:107 You will not see in her (the earth) any Crookedness (Bend/Curvature) or Ruggedness
(i.e, no surface features, it will appear smooth, the flat earth metric).
20:108 On a Day they will follow the Caller/Summoner, without Crookedness/Dishonestly/Evasion to Him, and the Voices will be Hushed/Overawed by the Merciful, and you'll not hear anything except murmurs/whispers/soughing sound.
Surah 46 Al-Ahqaf ( الْأَحْقَافِ , Curved Sand Dunes)
وَاذْكُرْ أَخَا عَادٍ إِذْ أَنذَرَ قَوْمَهُ بِالْأَحْقَافِ وَقَدْ خَلَتْالنُّذُرُ مِن بَيْنِ يَدَيْهِ
وَمِنْ خَلْفِهِ أَلَّا تَعْبُدُوا إِلَّا اللَّهَ
إِنِّي أَخَافُ عَلَيْكُمْ عَذَابَ يَوْمٍ عَظِيمٍ 46:21
46:21 And remember 'Aad's bretheren when He warned his people among the wind-Curved Sand Dunes, and indeed warners came and went before and after him, saying: 'Serve none but God. Truly, I fear for you the suffering of a Momentous/Significant/Great/Extraordinary Day'.
{Aside:You're asking me to do this and that's a steep apathy curve You expect me to get over after all these years---I Rest In God; and, since You been fronting me so long--after You my dear Alfonse! Besides, what's my motivation?
 |
| Pantograph |
He Says: Insolence!
She Says: I've just been talkin' to my Brothers Michael.
He Says: Every time I turn around I see you talking to one of them. How many brothers named Michael does a woman need?
She Says: All of''em!
He Says: All...ah? So, You're that One.
}
Ok, Ok... SO, Let's try a W-Curve...
A Pantograph is a jointed device for copying a plane figure to any desired scale. It incorporates a pair of face bows fixed to the jaws, used for inscribing centrically related points and arcs leading to the points on segments relatable to the three craniofacial planes.
A throw – in German ‘wurf’, refers to a series of four
points on a line which trace the 1-Dimensional motion of a point on a
projective line, the W-curve.
The term Throw (Wurf) was first introduced to
avoid the metrical implication of a ratio. The Algebra of Throws provides an approach to numerical propositions, usually taken as
axioms, but proven in projective geometry.
In the diagram ..., it turns out that the cross-ratio of a series of 4 points, taken in afixed order, does not depend on the choice of a line L, and is said to be invariant
of the 4-tuple of lines {Li}.This can be
understood as follows: if L and L′are two lines not passing through Q then the perspective transformationfrom L to L′with the center Q is a projective transformation thattakes the quadruple {Pi} of points on L into the quadruple {Pi′}of points on L′.
Therefore, the invariance of the cross-ratio under projective automorphisms of
the line implies (in fact, is equivalent to) the independence of the
cross-ratio of the four collinear points {Pi}
on the lines {Li} from the choice of the line that contains
them.
For points on a projective line (like
the W-curve), the cross-ratio, (aka, double ratio and anharmonic ratio), is a special number associated with such a series
of an ordered quadruple of collinear points.
If the four points
are represented in homogeneous coordinates by vectors (ie., objects that transform like first-rank tensors) a,b,c,d such that c=a+b
and d=ka+b, then their cross-ratio is k.
In the Cayley–Klein model of hyperbolic geometry, the distance between points is expressed in
terms of a certain cross-ratio.
{ For a generalized conic, in this case a unit circle, any two points in
the unit disk, p, q, the line connecting them
intersects the circle in two points, a and b. The
points are, in order,a, p, q, b. The distance between p and q in the Cayley–Klein model of
the plane hyperbolic geometry can
be expressed as
... (the factor 1/2 is needed to make
the curvature −1).}
In the language of group theory, the symmetric group S4 acts on the cross-ratio by
permuting coordinates. The kernel of this action is isomorphic to the Klein four-group K. This group consists of 2-cycle
permutations of type  (in addition to the identity), which preserve the cross-ratio. The
effective symmetry group is then the quotient group
(in addition to the identity), which preserve the cross-ratio. The
effective symmetry group is then the quotient group  , which is isomorphic to S3.
, which is isomorphic to S3.
 |
| The 6 Possible Values of the Cross-Ratio |
For certain values of λ there are fewer than 6 possible values of the 6 possible values of cross-ratio due to enhanced symmetry. These values of λ correspond to fixed points of the action of S3 on the Riemann sphere (given by the
above 6 functions); in other words, those points with a non-trivial stabilizer in this permutation group.
The first set of fixed points is
{0, 1, ∞}. However, the cross-ratio can never take on these values if the
points {zi} are all distinct. These values are limit values
as one pair of coordinates approach each other:
 |
Limit Values of Cross-Ratio
Due to Enhanced Symmetry Corresponding to Fixed Points |
The second set of fixed points is
{−1, 1/2, 2}--what is classically called the harmonic cross-ratio, and arises in projective harmonic conjugates.
In the real case, there are no other exceptional orbits (See About the Myth-tery, projection/buruj/zodiac).
The most symmetric cross-ratio
occurs when
l = e±ip/3
...the only possible values of the cross-ratio.
~~~~
Given the same starting point, find
the point midway between their terminal points, aka the harmonic
conjugate of infinity with regard to their terminal points, and then
find the harmonic conjugate of the initial point with regard to this mid-point
and infinity. Generalizing this to add throws (CA,BD) and (CA,BD' ),
then finding M the harmonic conjugate of C with
regard to D and D' , and then S the harmonic conjugate of A with regard to C and M :
A definition of the product of two
throws is derived in a similar fashion.
A summary statement is given by
Veblen & Young given by Theorem 10: "The set of points on a line, with P∞ removed,
forms a field with respect to the operations previously
defined".
 |
Horizontal Reflection
Retrograde Motion Outer Planet
Hand Drawn Freeform |
~ ~~ ~
 |
Outer Planet
Retrograde Motion |
Below is one Measure of Music Based on the Retrograde Motion of An Outer Planet (As Above).
 |
One Way to Set The Scale and Determine the Measure
Based on Retrograde Motion of an Outer Planet |
























